আসুন ত্রিমাত্রিক বস্তুর রহস্যভেদ করি!
আচ্ছা, চারপাশে তাকিয়ে দেখুন তো! আপনার মোবাইল ফোনটা? টেবিলটা? এমনকি আপনি নিজেও? এদের সবার মধ্যেই একটা জিনিস কমন, জানেন তো? এরা সবাই ত্রিমাত্রিক বস্তু! কিন্তু ত্রিমাত্রিক বস্তু আসলে কী, তাই তো ভাবছেন? চলুন, আজ এই বিষয়ে একটু খোলামেলা আলোচনা করা যাক। গণিতের জটিল সংজ্ঞা থেকে দূরে থেকে, আমরা চেষ্টা করব সহজ ভাষায় ত্রিমাত্রিক বস্তুর ধারণাটি বুঝিয়ে দিতে।
ত্রিমাত্রিক বস্তু কী? (What is a 3D Object?)
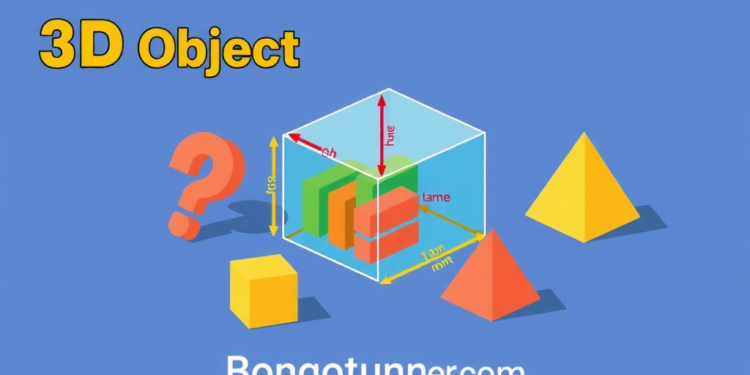
সহজ ভাষায় বলতে গেলে, যে বস্তুর দৈর্ঘ্য, প্রস্থ এবং উচ্চতা – এই তিনটি মাত্রা আছে, তাকেই ত্রিমাত্রিক বস্তু বলা হয়। মানে, জিনিসটা কতটা লম্বা, কতটা চওড়া আর কতটা উঁচু – এই তিনটি জিনিস মেপে বার করতে পারলেই সেটা থ্রিডি!
যেমন ধরুন, একটা ফুটবল। এর দৈর্ঘ্য আছে, প্রস্থ আছে, আর অবশ্যই উচ্চতাও আছে (যদিও ফুটবলের ক্ষেত্রে দৈর্ঘ্য, প্রস্থ, উচ্চতা সবই সমান, মানে ব্যাসার্ধ)। তাই ফুটবল একটি ত্রিমাত্রিক বস্তু।
- দৈর্ঘ্য (Length): বস্তুটির এক প্রান্ত থেকে অন্য প্রান্ত পর্যন্ত দূরত্ব।
- প্রস্থ (Width): বস্তুটির চওড়া দিকটা কতখানি।
- উচ্চতা (Height): ভূমি থেকে বস্তুটির উপরের দিকের দূরত্ব।
ত্রিমাত্রিক বস্তুর বৈশিষ্ট্য (Features of 3D Objects)
ত্রিমাত্রিক বস্তুর কিছু বিশেষ বৈশিষ্ট্য আছে, যা একে দ্বিমাত্রিক বস্তু থেকে আলাদা করে। এদের মধ্যে কয়েকটা গুরুত্বপূর্ণ বৈশিষ্ট্য আলোচনা করা হলো:
- আয়তন (Volume): একটি ত্রিমাত্রিক বস্তু কতটা জায়গা দখল করে, সেটাই তার আয়তন। যেমন, একটি বাক্সের ভেতরে কতটা জিনিস রাখা যাবে, তা তার আয়তন দিয়ে বোঝা যায়।
- ক্ষেত্রফল (Surface Area): ত্রিমাত্রিক বস্তুর বাইরের দিকের পুরো ক্ষেত্রফল হলো তার পৃষ্ঠের ক্ষেত্রফল। যেমন, একটা ফুটবলের বাইরের চামড়াটা পুরোটা মাপলে যা হবে।
- ভর (Mass): বস্তুর মধ্যে কতটা “stuff” আছে, মানে কতটুকু পদার্থ দিয়ে তৈরি, সেটাই তার ভর।
- আকৃতি (Shape): ত্রিমাত্রিক বস্তুর বিভিন্ন আকৃতি হতে পারে, যেমন গোল, বাক্স আকারের, চোঙা আকারের ইত্যাদি।
দৈনন্দিন জীবনে ত্রিমাত্রিক বস্তুর উদাহরণ (Examples of 3D Objects in Daily Life)
আমাদের চারপাশে অজস্র ত্রিমাত্রিক বস্তু ছড়িয়ে আছে। কিছু সাধারণ উদাহরণ নিচে দেওয়া হলো:
- ঘরবাড়ি: আপনি যে ঘরে বসে এই লেখাটি পড়ছেন, সেটি একটি ত্রিমাত্রিক বস্তু। এর দৈর্ঘ্য, প্রস্থ এবং উচ্চতা সবই আছে।
- আসবাবপত্র(Furniture): চেয়ার, টেবিল, খাট – এগুলো সবই ত্রিমাত্রিক বস্তু।
- খাবার জিনিস(Food Items): ফল, সবজি, রুটি – এগুলোও ত্রিমাত্রিক, যদিও এদের আকার সবসময় নির্দিষ্ট নাও হতে পারে।
- যানবাহন(Vehicles): গাড়ি, বাস, ট্রেন, সাইকেল – সবই ত্রিমাত্রিক বস্তু।
কিছু পরিচিত ত্রিমাত্রিক আকারের বর্ণনা (Description of Some Common 3D Shapes)
গণিতে কিছু নির্দিষ্ট আকারের ত্রিমাত্রিক বস্তু নিয়ে আলোচনা করা হয়। এদের কয়েকটির সংক্ষিপ্ত বর্ণনা নিচে দেওয়া হল:
- গোলক (Sphere): ফুটবলের মতো দেখতে। এর সব বিন্দু কেন্দ্র থেকে সমান দূরে থাকে।
- ঘনক (Cube): লুডুর ছক্কার মতো। এর ৬টা দিকই বর্গক্ষেত্র।
- আয়তাকার ঘনবস্তু (Cuboid): ইটের মতো। এর ৬টা দিক আয়তক্ষেত্র।
- চোঙ (Cylinder): পাইপের মতো। এর দুটো দিক বৃত্তাকার এবং একটি দিক বাঁকানো।
- শঙ্কু (Cone): আইসক্রিমের কোনের মতো। এর একটি দিক বৃত্তাকার এবং অন্য দিকটি ক্রমশ সরু হয়ে একটি বিন্দুতে মেশে।
ত্রিমাত্রিক বস্তু চেনার সহজ উপায় (Easy Ways to Identify 3D Objects)
কোনো বস্তু ত্রিমাত্রিক কিনা, তা চেনার সহজ উপায় হলো দেখা যে বস্তুটির তিনটি মাত্রা আছে কিনা – দৈর্ঘ্য, প্রস্থ এবং উচ্চতা। যদি এই তিনটি জিনিস মাপা যায়, তাহলে সেটি ত্রিমাত্রিক বস্তু। এছাড়াও, ত্রিমাত্রিক বস্তুকে বিভিন্ন দিক থেকে দেখা যায়, যা দ্বিমাত্রিক বস্তুর ক্ষেত্রে সম্ভব নয়।
ত্রিমাত্রিক জ্যামিতি (Three-Dimensional Geometry)
ত্রিমাত্রিক জ্যামিতি হলো গণিতের সেই শাখা, যেখানে ত্রিমাত্রিক বস্তু এবং তাদের বৈশিষ্ট্য নিয়ে আলোচনা করা হয়। এই জ্যামিতি ব্যবহার করে ত্রিমাত্রিক বস্তুর আয়তন, ক্ষেত্রফল, আকৃতি ইত্যাদি নির্ণয় করা যায়।
ত্রিমাত্রিক স্থানাঙ্ক ব্যবস্থা (Three-Dimensional Coordinate System)
ত্রিমাত্রিক স্থানাঙ্ক ব্যবস্থায় তিনটি অক্ষ (x, y, z) থাকে, যা পরস্পর লম্বভাবে অবস্থিত। এই অক্ষগুলো ব্যবহার করে ত্রিমাত্রিক স্থানে কোনো বিন্দুর অবস্থান নির্ণয় করা যায়।
ত্রিমাত্রিক স্থানাঙ্ক ব্যবস্থায় একটি বিন্দুর অবস্থান তিনটি সংখ্যা দ্বারা চিহ্নিত করা হয়, যা (x, y, z) আকারে লেখা হয়। এখানে,
- x হলো x-অক্ষ বরাবর বিন্দুর দূরত্ব,
- y হলো y-অক্ষ বরাবর বিন্দুর দূরত্ব, এবং
- z হলো z-অক্ষ বরাবর বিন্দুর দূরত্ব।
ত্রিমাত্রিক বস্তুর গঠন (Construction of 3D Objects)
ত্রিমাত্রিক বস্তু তৈরি করার জন্য বিভিন্ন পদ্ধতি ব্যবহার করা হয়। এর মধ্যে কিছু উল্লেখযোগ্য পদ্ধতি হলো:
- ত্রিমাত্রিক মুদ্রণ (3D Printing): এই পদ্ধতিতে কম্পিউটার-নিয়ন্ত্রিত মেশিনের সাহায্যে একটির পর একটি স্তর ফেলে ত্রিমাত্রিক বস্তু তৈরি করা হয়।
- ছাঁচনির্মাণ (Molding): গলিত পদার্থকে ছাঁচে ফেলে ঠান্ডা করে ত্রিমাত্রিক বস্তু তৈরি করা হয়।
- কাটিং এবং জোড়া লাগানো (Cutting and Assembling): বিভিন্ন অংশ কেটে সেগুলোকে একসঙ্গে জোড়া দিয়ে ত্রিমাত্রিক বস্তু তৈরি করা হয়।
ত্রিমাত্রিক বস্তুর ব্যবহার (Uses of 3D Objects)
ত্রিমাত্রিক বস্তুর ব্যবহার ব্যাপক ও বহুমুখী। নিচে কয়েকটি উল্লেখযোগ্য ক্ষেত্র উল্লেখ করা হলো:
- প্রকৌশল (Engineering): ত্রিমাত্রিক মডেলিং ব্যবহার করে বিভিন্ন কাঠামো, যন্ত্রাংশ এবং নকশা তৈরি করা হয়।
- চিকিৎসা বিজ্ঞান (Medical Science): ত্রিমাত্রিক ইমেজিং ব্যবহার করে শরীরের অভ্যন্তরীণ অঙ্গপ্রত্যঙ্গ দেখা এবং রোগ নির্ণয় করা হয়।
- স্থাপত্য (Architecture): ত্রিমাত্রিক মডেল ব্যবহার করে বিল্ডিং এবং অন্যান্য স্থাপত্যের নকশা তৈরি করা হয়।
- ভিডিও গেমস ও সিনেমা (Video Games and Movies): ত্রিমাত্রিক গ্রাফিক্স ব্যবহার করে বাস্তবসম্মত দৃশ্য তৈরি করা হয়।
বিভিন্ন ক্ষেত্রে ত্রিমাত্রিক মডেলিং-এর গুরুত্ব (Importance of 3D Modeling in Various Fields)
ত্রিমাত্রিক মডেলিং বিভিন্ন ক্ষেত্রে গুরুত্বপূর্ণ ভূমিকা রাখে। এর মাধ্যমে কোনো বস্তুকে ত্রিমাত্রিকভাবে উপস্থাপন করা যায়, যা ডিজাইন এবং নির্মাণের ক্ষেত্রে খুবই উপযোগী। নিচে কয়েকটি উদাহরণ দেওয়া হলো:
- পণ্য ডিজাইন (Product Design): নতুন পণ্য ডিজাইন করার সময় ত্রিমাত্রিক মডেলিং ব্যবহার করে পণ্যের ত্রুটিগুলো আগে থেকেই চিহ্নিত করা যায়।
- বাস্তুবিদ্যা (Architecture): ত্রিমাত্রিক মডেলিংয়ের মাধ্যমে একটি বিল্ডিংয়ের ভেতরের এবং বাইরের গঠন সঠিকভাবে বোঝা যায়।
- শিক্ষা (Education): ত্রিমাত্রিক মডেলিং ব্যবহার করে জটিল বিষয়গুলো সহজে শিক্ষার্থীদের বোঝানো যায়।
কিছু সাধারণ জিজ্ঞাসা (Frequently Asked Questions – FAQs)
এখানে ত্রিমাত্রিক বস্তু নিয়ে কিছু সাধারণ প্রশ্নের উত্তর দেওয়া হলো:
ত্রিমাত্রিক বস্তু এবং দ্বিমাত্রিক বস্তুর মধ্যে পার্থক্য কী? (What is the difference between a 3D object and a 2D object?)
মূল পার্থক্য হলো মাত্রার সংখ্যা। ত্রিমাত্রিক বস্তুর তিনটি মাত্রা (দৈর্ঘ্য, প্রস্থ, উচ্চতা) থাকে, যেখানে দ্বিমাত্রিক বস্তুর মাত্র দুটি মাত্রা (দৈর্ঘ্য, প্রস্থ) থাকে। একটা কাগজের ছবি হলো দ্বিমাত্রিক, কারণ এর বেধ (উচ্চতা) প্রায় নেই বললেই চলে।
ত্রিমাত্রিক বস্তুর আয়তন কীভাবে নির্ণয় করা হয়? (How is the volume of a 3D object determined?)
বিভিন্ন আকারের ত্রিমাত্রিক বস্তুর আয়তন নির্ণয়ের জন্য আলাদা সূত্র আছে। যেমন, ঘনকের আয়তন হলো বাহুর দৈর্ঘ্য-এর ঘন (side^3), আর গোলকের আয়তন হলো (4/3)πr^3 (যেখানে r হলো ব্যাসার্ধ)।
সব আকার কি ত্রিমাত্রিক হতে পারে? (Can all shapes be three-dimensional?)
গণিতগতভাবে, এমন অনেক আকার আছে যা ত্রিমাত্রিক নয়, যেমন বিন্দু (Point) এবং রেখা (Line)। কিন্তু বাস্তবে, আমাদের চারপাশে যা কিছু দেখি, তার সবই কোনো না কোনোভাবে ত্রিমাত্রিক।
ত্রিমাত্রিক বস্তুর উদাহরণ দিন।(Give Three Dimensional object examples.)
একটা বই, একটা ইট ,একটি ফুটবল, আপনার পড়ার টেবিল এবং আপনি নিজেও ত্রিমাত্রিক বস্তু।
ত্রিমাত্রিক বস্তুর সংজ্ঞা কি?(What is the definition of a three-dimensional object?)
যে বস্তুর দৈর্ঘ্য, প্রস্থ এবং উচ্চতা – এই তিনটি মাত্রা আছে, তাকেই ত্রিমাত্রিক বস্তু বলা হয়।
ত্রিমাত্রিক বস্তু কিভাবে তৈরি করা হয়?(How are three-dimensional objects made?)
ত্রিমাত্রিক বস্তু বিভিন্ন উপায়ে তৈরি করা যায় যেমন: ত্রিমাত্রিক মুদ্রণ (3D Printing), ছাঁচনির্মাণ (Molding), কাটিং এবং জোড়া লাগানো (Cutting and Assembling).
উপসংহার (Conclusion)
তাহলে, ত্রিমাত্রিক বস্তু আসলে আমাদের চারপাশের জগতেরই একটা অংশ। এদের বৈশিষ্ট্য, ব্যবহার এবং গঠন প্রক্রিয়া জানা আমাদের জন্য খুবই দরকারি। এই ব্লগ পোস্টে আমরা ত্রিমাত্রিক বস্তুর মূল ধারণাগুলো সহজ ভাষায় আলোচনা করার চেষ্টা করেছি। আশা করি, এই আলোচনা আপনাদের ত্রিমাত্রিক জগতকে আরও ভালোভাবে বুঝতে সাহায্য করবে।
এইবার আপনার পালা! চারপাশে তাকিয়ে দেখুন, আর খুঁজে বের করার চেষ্টা করুন আর কী কী জিনিস ত্রিমাত্রিক। কেমন লাগলো এই আলোচনা, তা জানাতে ভুলবেন না কিন্তু! আপনার মতামত আমাদের কাছে খুবই গুরুত্বপূর্ণ।